Binary Tree
I. DFS
Template
class TreeNode {
int val;
TreeNode left, right;
}
void traverse(TreeNode root) {
if (root == null) {
return;
}
// Pre-order
traverse(root.left);
// In-order
traverse(root.right);
// Post-order
}
Example
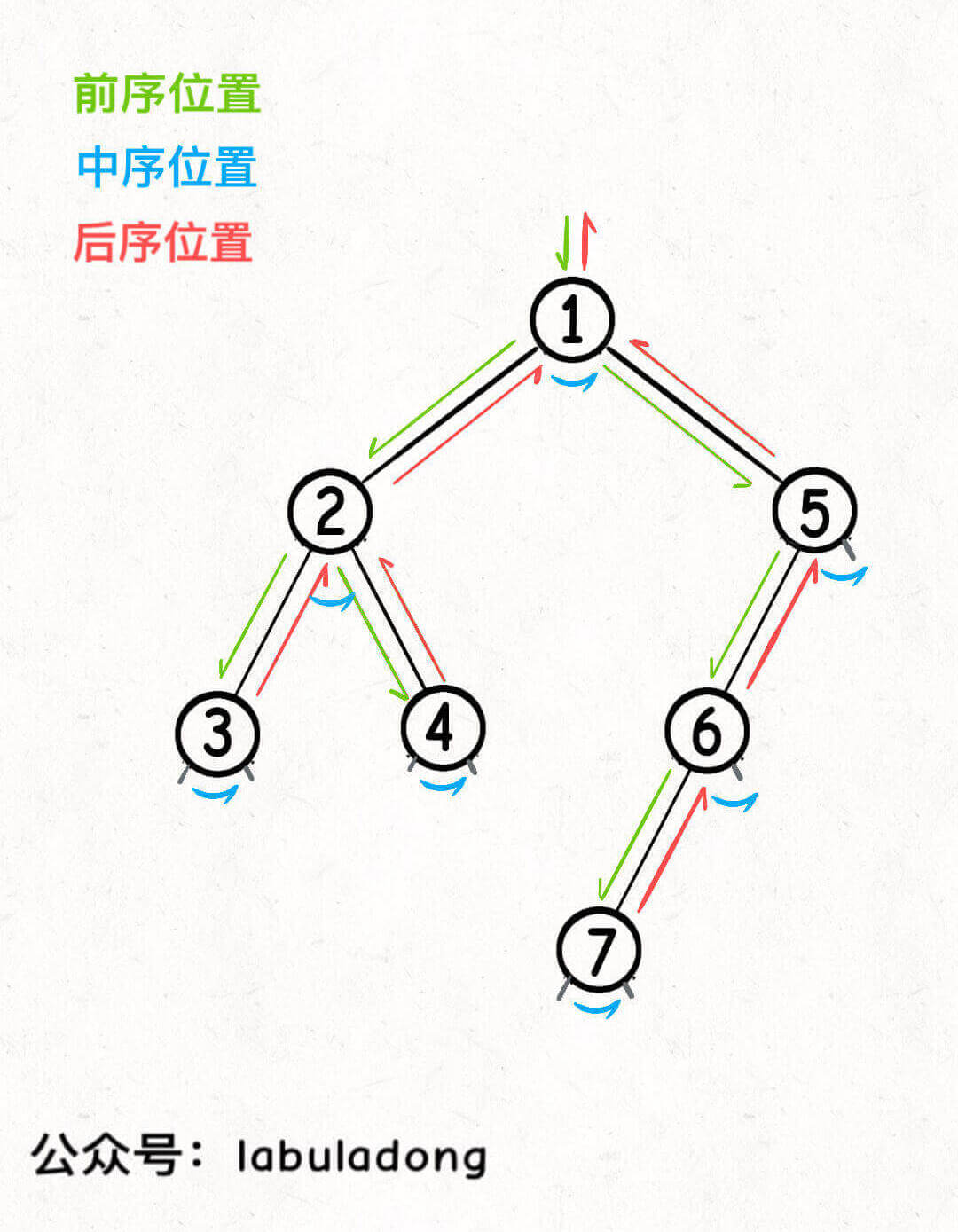
- Pre-order: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7
- In-order: 3 -> 2 -> 4 -> 1 -> 7 -> 6 -> 5
- Post-order: 3 -> 4 -> 2 -> 7 -> 6 -> 5 -> 1
II. BFS
Template
void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
// 访问 cur 节点
System.out.println(cur.val);
// 把 cur 的左右子节点加入队列
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}
}
- 把队列中的所有节点都出队,再把当前节点的左右子节点加入队列
III. Post-order Position
LeetCode 110. Balanced Binary Tree(Easy)
Idea
- 每一個node的左右子榭的深度差
Code
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
if (checkHeight(root) == -1) return false;
return true;
}
int checkHeight(TreeNode root) {
if (root == null) return 0;
int leftHeight = checkHeight(root.left);
int rightHeight = checkHeight(root.right);
if (leftHeight == -1 || rightHeight == -1) return -1;
if (Math.abs(leftHeight - rightHeight) > 1) return -1;
return Math.max(leftHeight, rightHeight) + 1;
}
LeetCode 543. Diameter of Binary Tree(Easy)
Idea
- 找一個節點的左右子樹最大深度之和
Code (Slow)
class Solution {
// 记录最大直径的长度
int maxDiameter = 0;
public int diameterOfBinaryTree(TreeNode root) {
// 对每个节点计算直径,求最大直径
traverse(root);
return maxDiameter;
}
// 遍历二叉树
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 对每个节点计算直径
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
int myDiameter = leftMax + rightMax;
// 更新全局最大直径
maxDiameter = Math.max(maxDiameter, myDiameter);
traverse(root.left);
traverse(root.right);
}
// 计算二叉树的最大深度
int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
return 1 + Math.max(leftMax, rightMax);
}
}
traverse- Recursively visits every node in the tree.
- For each node, it:
- Calls maxDepth on the left and right subtrees to compute their depths.
Code (Fast)
class Solution {
// 记录最大直径的长度
int maxDiameter = 0;
public int diameterOfBinaryTree(TreeNode root) {
maxDepth(root);
return maxDiameter;
}
int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
// 后序位置,顺便计算最大直径
int myDiameter = leftMax + rightMax;
maxDiameter = Math.max(maxDiameter, myDiameter);
return 1 + Math.max(leftMax, rightMax);
}
}
- The maxDepth method is called exactly once for each node in the tree during the post-order traversal
IV. Lowest Common Ancestor (LCA)
Find one target in non-duplicate binary tree
TreeNode find(TreeNode root, int target) {
if (root == null) return null;
if (root.val == target) return root;
TreeNode left = find(root.left, target);
if (left != null) return left;
TreeNode right = find(root.right, target);
if (right != null) return right;
return null;
}
Find two targets in non-duplicate binary tree
TreeNode find(TreeNode root, int val1, int val2) {
if (root == null) return null;
if (root.val == val1 || root.val== val2) return root;
TreeNode left = find(root.left, val1, val2);
TreeNode right = find(root.right, val1, val2);
return left != null ? left : right;
}
LeetCode 236. Lowest Common Ancestor of a Binary Tree(Medium)
Idea
- 如果一個節點能夠在它左右子數中分別找到
pandq,該節點為LCA - 題目說了
p&q一定存在於樹中,所以遇到q可以直接return,根本没遍历到 p,也依然可以断定 p 在 q 底下,q 就是 LCA 节点。
Code
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return find(root, p.val, q.val);
}
// 在二叉树中寻找 val1 和 val2 的最近公共祖先节点
TreeNode find(TreeNode root, int val1, int val2) {
if (root == null) {
return null;
}
// 前序位置
if (root.val == val1 || root.val == val2) {
// 如果遇到目标值,直接返回
return root;
}
TreeNode left = find(root.left, val1, val2);
TreeNode right = find(root.right, val1, val2);
// 后序位置,已经知道左右子树是否存在目标值
if (left != null && right != null) {
// 当前节��点是 LCA 节点
return root;
}
return left != null ? left : right;
}
Mindset
important
- By Traverse: Can you obtain the answer by traversing the binary tree once? If so, use a traverse function with external variables to achieve this, which is the "traversal" mindset.
- By Problem Decomposition: Can you define a recursive function to derive the answer to the original problem from the answers to subproblems (subtrees)? If so, write out the definition of this recursive function and make full use of its return value, which is the "problem decomposition" mindset.
- Regardless of the mindset used, you need to consider: What does an individual binary tree node need to do? When (pre/in/post-order position) should it do this? You don't need to worry about other nodes; the recursive function will perform the same operations on all nodes.
LeetCode 226. Invert Binary Tree(Easy)
-
By Traverse
public TreeNode invertTree(TreeNode root) {
// Exchange the left and right child of each node
traverse(root);
return root;
}
void traverse(TreeNode root) {
if (root == null) {
return;
}
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
traverse(root.left);
traverse(root.right);
} -
By Problem Decomposition
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode left = invertTree(root.left);
TreeNode right = invertTree(root.right);
root.left = right;
root.right = left;
// 和定义逻辑自恰:以 root 为根的这棵二叉树已经被翻转,返回 root
return root;
}
LeetCode 116. Populating Next Right Pointers in Each Node
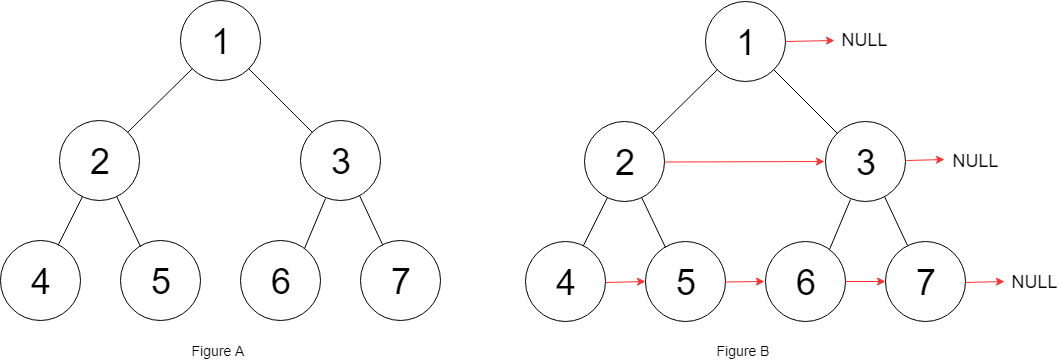
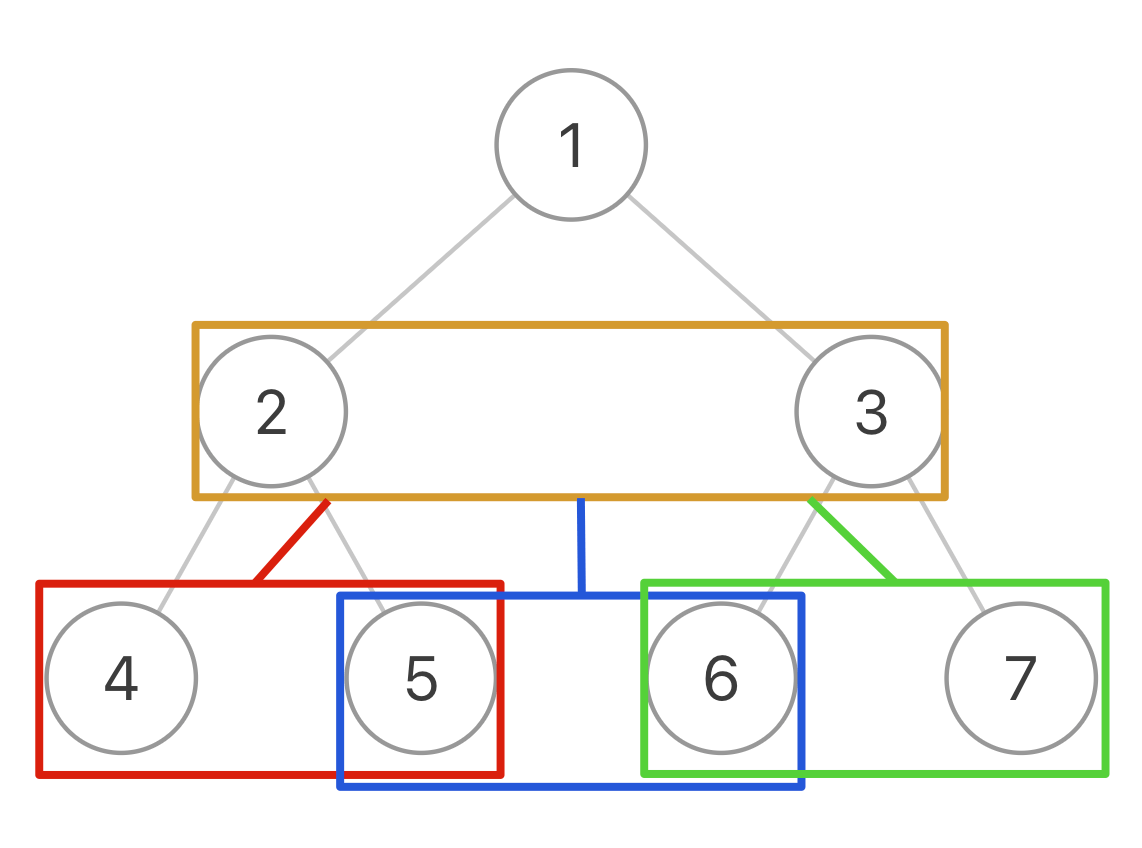
public Node connect(Node root) {
if (root == null) return null;
traverse(root.left, root.right);
return root;
}
void traverse(Node left, Node right) {
if (node1 == null || node2 == null) {
return;
}
node1.next = node2;
// 连接相同父节点的两个子节点
traverse(node1.left, node1.right);
traverse(node2.left, node2.right);
// 连接跨越父节点的两个子节点
traverse(node1.right, node2.left);
}
LeetCode 102. Binary Tree Level Order Traversal (Medium)
- Use BFS template easily solved
Type: Construct Binary Tree
- Idea: 先找到根节点,然后找到并递归构造左右子树即可。
LeetCode 654. Maximum Binary Tree (Medium)
Step
- Find the
maxValin the array - Create a node with
maxVal - Contruct the left subtree by the array to the left of
maxVal - Construct the right subtree by the array to the right of
maxVal
Code
public TreeNode constructMaximumBinaryTree(int[] nums) {
return build(nums, 0, nums.length - 1);
}
TreeNode build(int[] nums, int left, int right) {
// base case
if (left > right) return null;
// find the maxVal in the array
int index = -1, maxVal = Integer.MIN_VALUE;
for (int i = left; i <= right; i++) {
if (maxVal < nums[i]) {
index = i;
maxVal = nums[i];
}
}
TreeNode root = new TreeNode(maxVal);
root.left = build(nums, left, index - 1);
root.right = build(nums, index + 1, right);
return root;
}
LeetCode 105. Construct Binary Tree from Preorder and Inorder Traversal (Medium)
Idea
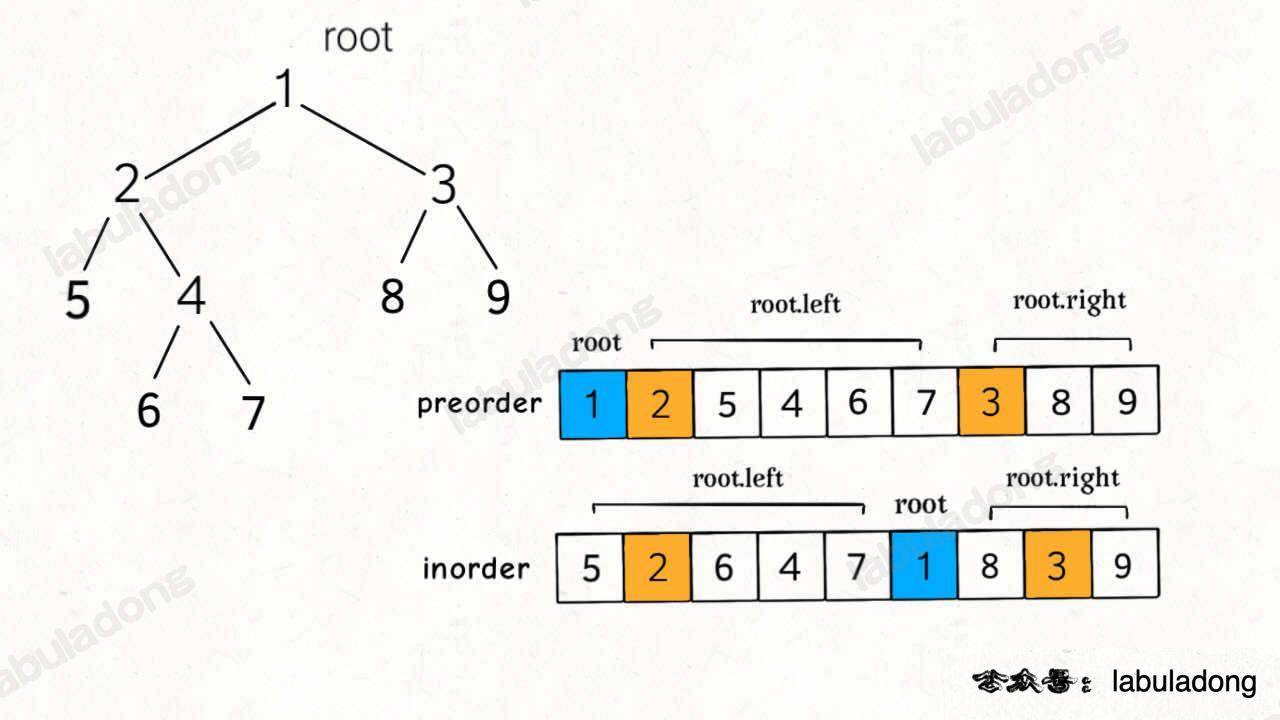

- root: can be obtained from preorder
- left/right subtree: can be obtained from inorder

- 搵left/right subtree的index for 定義inorder 的range

- 搵left/right subtree的index for 定義opreorder 的range
LeetCode 110. Balanced Binary Tree (Easy)
Idea
- For each node:
- Recursively checks left and right subtrees
- Returns -1 if either subtree is unbalanced
- Checks if the height difference between left and right subtrees is > 1
- If balanced, returns the height (Math.max(left, right) + 1)