Skip to main content

Binary Search

Step​

  1. Use two points left and right to reduce the serach range
  2. Find the middle point mid

Implementation​

    public int binarySearch(int[] nums, int target) {
        int left = 0, right = nums.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            }
        }
    }

Why use left <= right instead of left < right?​

  • right is nums.length - 1, points to the last element in the array. If right is nums.length，it would be index out of bound.
  • The former one is [left, right]，the later one is [left, right)
  • We here use the former one as the search range
  • The termination condition of left <= right is left = right + 1，e.g.[3, 2]，區間為空
  • The termination condition of left < right is left = right，e.g.[3, 3]，區間不為空
    • Special handling 
          // ...
          while (left < right) {
              // ...
          }
          return nums[left] == target ? left : -1;

Why left = mid + 1, right = mid - 1?​

  • Our search space is [left, right]
  • When we find nums[mid] != target, we go search in [left, mid - 1] or [mid + 1, right]
  • Because we already search nums[mid], so we should remove it from search space

II. Left-Bounded Binary Search ([left, right))​

Implementation​

    int left_bound(int[] nums, int target) {
        int left = 0;
        // 注意
        int right = nums.length;
        
        // 注意
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                right = mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                // 注意
                right = mid;
            }
        }
        return left;
    }

Why use < instead of <=?​

  • As right = nums.length, the search space in every iteration is [left, right)
  • The termination condition is left == right, the search space is 0, e.g. [2, 2)

Why left = mid + 1 and right = mid?​

  • Our search space is [left, right)
  • So after we check nums[mid] and find it is not equal to target, we go to the left side of mid and right side of mid
  • go to the right side of mid: [mid + 1, right)
  • go to the left side of mid: [left, mid)

Why does this algorithm find the left boundary?​

  • It do not return the index of the target when we find the target
  • Instead, we narrow the upper bound of the search space
    if (nums[mid] == target) {
        right = mid;
    }

Why return left instead of right?​

  • Both are the same because the while loop ends when left == right

III. Left-Bounded Binary Search ([left, right])​

Implementation​

    int leftBound(int[] nums, int target) { 
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            
            if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] == target) {
                right = mid - 1;
            }
        }

        if (left < 0 || left >= nums.length) {
            return -1;
        }
        return nums[left] == target ? left : -1;
    }

IV. Right-Bounded Binary Search ([left, right))​

Implementation​

    int right_bound(int[] nums, int target) {
        int left = 0, right = nums.length;
        
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                // 注意
                left = mid + 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid;
            }
        }
        // 注意
        if (left - 1 < 0 || left -  1 >= nums.length) {
            return -1;
        }
        return nums[left - 1] == target ? left - 1 : -1;
    }

Why return left - 1?​

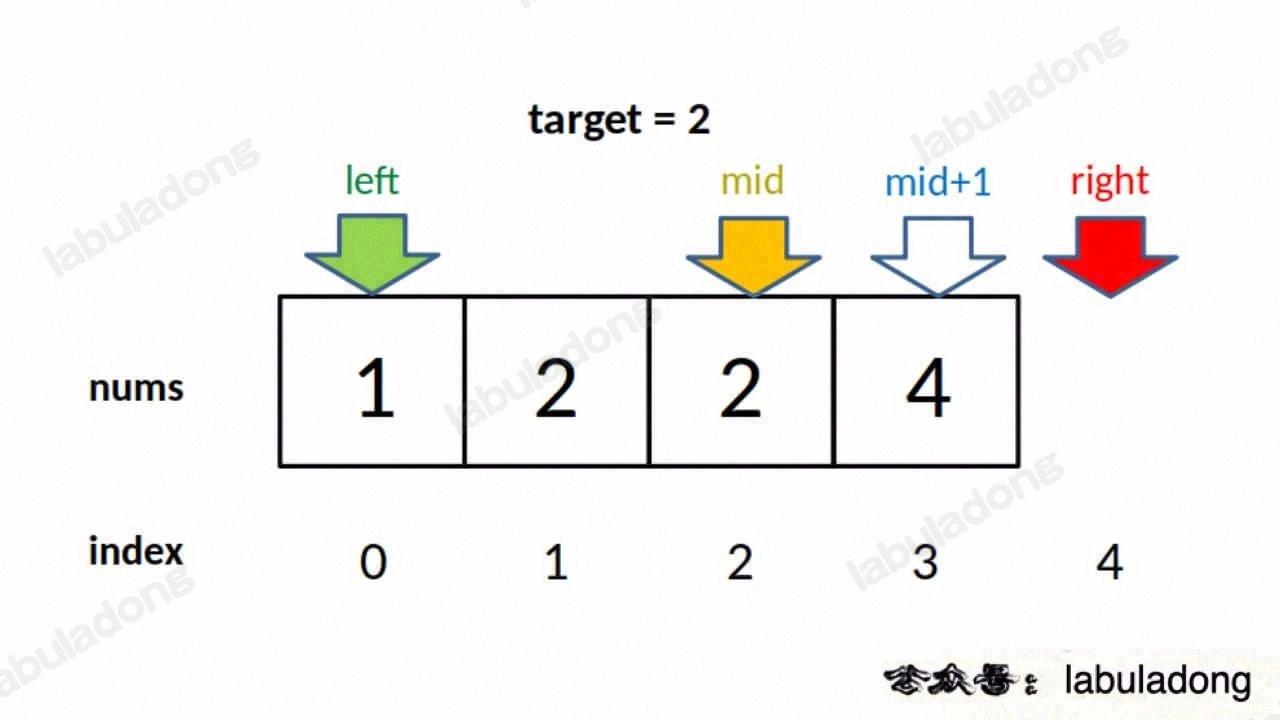
right-bounder

    if (nums[mid] == target) {
        left = mid + 1;
        // think it as: mid = left - 1
    }
  • When the while loop end, left become mid + 1. nums[left] is the equal to target (as in the image), and nums[left - 1] could be the target

Summary​

    因为我们初始化 right = nums.length - 1
    所以决定了我们的「搜索区间」是 [left, right]
    所以决定了 while (left <= right)
    同时也决定了 left = mid+1 和 right = mid-1

    因为我们只需找到一个 target 的索引即可
    所以当 nums[mid] == target 时可以立即返回
    因为我们初始化 right = nums.length
    所以决定了我们的「搜索区间」是 [left, right)
    所以决定了 while (left < right)
    同时也决定了 left = mid + 1 和 right = mid

    因为我们需找到 target 的最左侧索引
    所以当 nums[mid] == target 时不要立即返回
    而要收紧右侧边界以锁定左侧边界
    因为我们初始化 right = nums.length
    所以决定了我们的「搜索区间」是 [left, right)
    所以决定了 while (left < right)
    同时也决定了 left = mid + 1 和 right = mid

    因为我们需找到 target 的最右侧索引
    所以当 nums[mid] == target 时不要立即返回
    而要收紧左侧边界以锁定右侧边界

    又因为收紧左侧边界时必须 left = mid + 1
    所以最后无论返回 left 还是 right，必须减一

Reference​