Two-Pointer (Linked List)
1. LeetCode 21. Merge Two Sorted Lists
- https://leetcode.com/problems/merge-two-sorted-lists/
- Use dummy node
dummy node, no need to handle null pointer
use when you need to return a new linked list
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode dummy = new ListNode(-1);
ListNode p = dummy;
...
return dummy.next;
}
2. LeetCode 86. Partition List
- https://leetcode.com/problems/partition-list/
- Merging two in-ordered linkedlist
public ListNode partition(ListNode head, int x) {
// to store Node < x
ListNode dummy1 = new ListNode(-1);
// to store Node >= x
ListNode dummy2 = new ListNode(-1);
// p1 and p2 for returning the result
ListNode p1 = dummy1, p2 = dummy2;
ListNode p = head;
while (p != null) {
if (p.val >= x) {
p2.next = p;
p2 = p2.next;
} else {
p1.next = p;
p1 = p1.next;
}
// to break up the remaining nodes in p
ListNode temp = p.next;
p.next = null;
p = temp;
}
p1.next = dummy2.next;
return dummy1.next;
}
要將原linked list的node斷關
3. LeetCode 23. Merge k Sorted Lists
public ListNode mergeKLists(ListNode[] lists) {
if (lists.length == 0) return null;
ListNode dummy = new ListNode(-1);
ListNode p = dummy;
// 创建一个优先级队列,将所有链表的头节点加入队列
PriorityQueue<ListNode> pq = new PriorityQueue<>(
lists.length, (a, b)->(a.val - b.val));
// 遍历队列,将队列中的Head加入链表
for (ListNode head : lists) {
if (head != null) {
pq.offer(head);
}
}
while (!pq.isEmpty()) {
ListNode node = pq.poll();
p.next = node;
if (node.next != null) {
pq.add(node.next);
}
p = p.next;
}
return dummy.next;
}
Put all head nodes into a priority queue as min heap, so we can get the smallest node among all k lists. Time Complexity: O(Nlogk)
- In
pq, the size of queue is k, so the time complexity ofpoll()andadd()is O(logk). - All nodes are traversed once, so the time complexity of
whileloop is O(N).
4. LeetCode 19. Remove Nth Node From End of List
public ListNode removeNthFromEnd(ListNode head, int n) {
// 虚拟头结点
ListNode dummy = new ListNode(-1);
dummy.next = head;
// 删除倒数第 n 个,要先找倒数第 n + 1 个节点
ListNode x = findFromEnd(dummy, n + 1);
// 删掉倒数第 n 个节点
x.next = x.next.next;
return dummy.next;
}
private ListNode findFromEnd(ListNode head, int k) {
ListNode p1 = head;
// p1 先走 k 步
for (int i = 0; i < k; i++) {
p1 = p1.next;
}
ListNode p2 = head;
// p1 和 p2 同时走 n - k 步
while (p1 != null) {
p2 = p2.next;
p1 = p1.next;
}
// p2 现在指向第 n - k + 1 个节点,即倒数第 k 个节点
return p2;
}
- If you want to delete the nth node from the end, you need to find the (n + 1)th node from the head
- The reason to use dummy head is to prevent null pointer.
- Let say we have a linked list: 1 -> 2 -> 3 -> 4 -> 5, and you are required to delete the 5th node from the end.
- In this case, you need to find the 6th node from the head, which is not possible.
5. LeetCode 876. Middle of the Linked List
- https://leetcode.cn/problems/middle-of-the-linked-list/description/
- Slow pointer: move one step at a time
- Fast pointer: move two steps at a time
- Because
fastmoves twice as fast, whenfastreaches the end,slowwill be in the middle.
6. Detect Cycle in Ring
- Use above technique
- Linked List with Ring: it does not end with
null - If fast pointer can reach the end of list(i.e.
null) -> the list has no cycle - If the fast pointer catches up the slow pointer (meet at the same node), it means the fast pointer has looped around in a cycle
public boolean hasCycle(ListNode head) {
// 快慢指针初始化指向 head
ListNode slow = head, fast = head;
// 快指针走到末尾时停止
while (fast != null && fast.next != null) {
// 慢指针走一步,快指针走两步
slow = slow.next;
fast = fast.next.next;
// 快慢指针相遇,说明含有环
if (slow == fast) {
return true;
}
}
// 不包含环
return false;
}
- LeetCode 142. Linked List Cycle
public ListNode detectCycle(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;
}
// 上面的代码类似 hasCycle 函数
if (fast == null || fast.next == null) {
// fast 遇到空指针说明没有环
return null;
}
// 重新指向头结点
slow = head;
// 快慢指针同步前进,相交点就是环起点
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}- Suppose the slow pointer has traveled k steps when fast and slow meet
- it means fast has traveled 2k steps
- the extra k step (2k - k) must be a multiple of the cycle's length
7. LeetCode 160. Intersection of Two Linked Lists
-
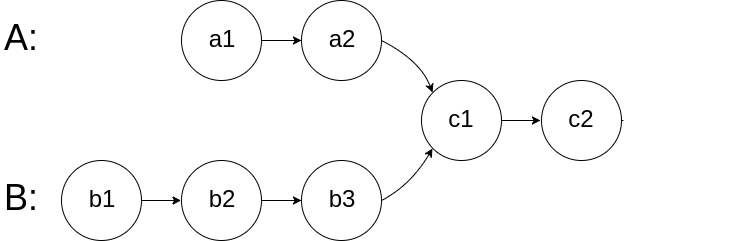
-
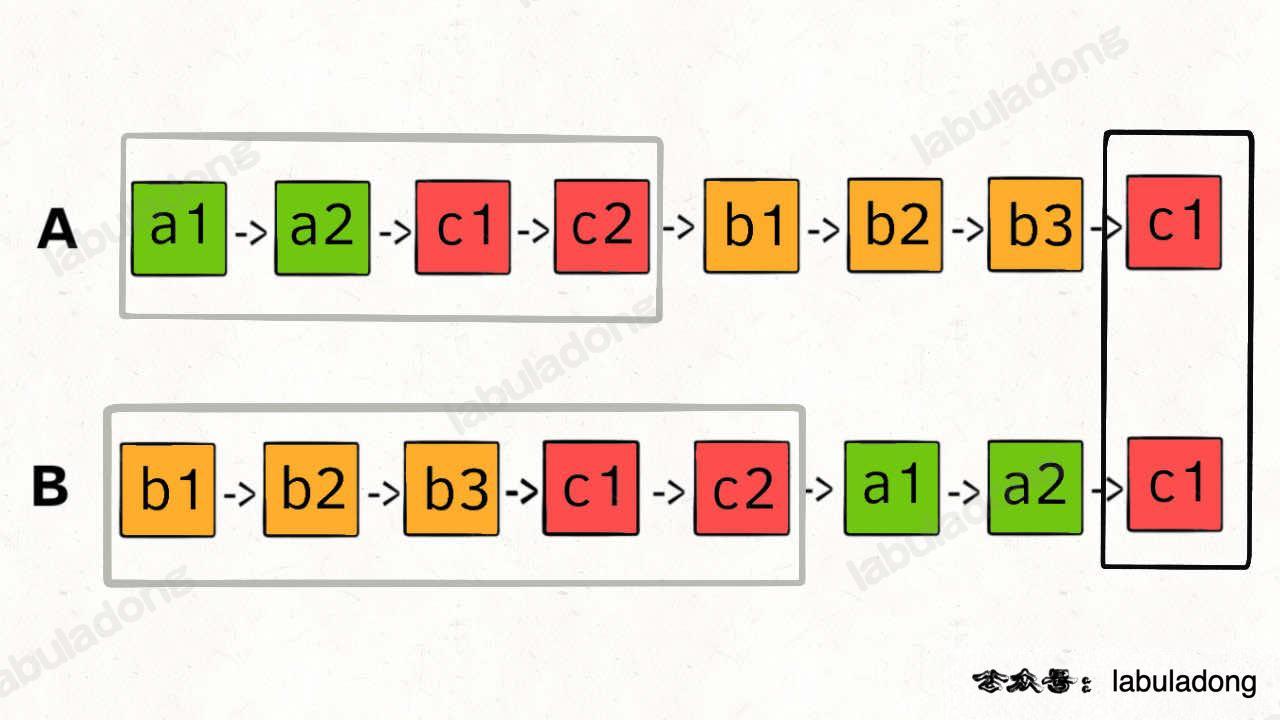
-
If no intersection exists, the two pointers will meet at the end of the list (null)
- A: a1 -> a2 -> c1 -> c2 -> b1 -> b2 -> b3 -> c3 -> c4 -> null
- B: b1 -> b2 -> b3 -> c3 -> c4 -> a1 -> a2 -> c1 -> c2 -> null
8. LeetCode 82. Remove Duplicates from Sorted List II
-
分解為two linked lists: 1) Unique List 2) Duplicated List
-
then return the head of unique list
-
what is duplicate?
- the value of current node equals the value of next node
- the value of current node = the value of last node in duplicate list
public ListNode deleteDuplicates(ListNode head) {
// / 运用虚拟头结点技巧,题目说了 node.val <= 100,所以用 101 作为虚拟头结点
ListNode dummyUniq = new ListNode(101);
ListNode dummyDup = new ListNode(101);
ListNode pUniq = dummyUniq, pDup = dummyDup;
ListNode p = head;
while (p != null) {
if ((p.next != null && p.val == p.next.val) || p.val == pDup.val) {
// 发现重复节点,接到重复链表后面
pDup.next = p;
pDup = pDup.next;
} else {
// 不是重复节点,接到不重复链表后面
pUniq.next = p;
pUniq = pUniq.next;
}
p = p.next;
// 将原链表和新链表断开
pUniq.next = null;
pDup.next = null;
}
return dummyUniq.next;
}
9. LeetCode 264. Ugly Number II
- Ugly Number: with prime factors only 2, 3, 5
- Expected linked list: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 8 -> ...
- Think it as linked list
- 2: 1 -> 12 -> 22 -> 3*2 -> ...
- 3: 1 -> 13 -> 23 -> 3*3 -> ...
- 5: 1 -> 15 -> 25 -> 3*5 -> ...
- 把這3條有序的linked list合併,need to remove duplicated value, e.g. 23 and 32
public int nthUglyNumber(int n) {
// pointer to the head of each linked list
int p2 = 1, p3 = 1, p5 = 1;
// the value of the head node of each linked list
int product2 = 1, product3 = 1, product5 = 1;
// the final merged linked list
int[] ugly = new int[n + 1];
// the pointer to the merged linked list
int p = 1;
while (p <= n) {
int min = Math.min(product2, Math.min(product3, product5));
// add the result list
ugly[p] = min;
p++;
// if the node is selected from the 2nd list, then move the pointer to the next node in 2nd list
// if the value of head node of any other list is equal to the value of the selected node, then move the pointer to the next node in that list
if (min == product2) {
product2 = 2 * ugly[p2];
p2++;
}
if (min == product3) {
product3 = 3 * ugly[p3];
p3++;
}
if (min == product5) {
product5 = 5 * ugly[p5];
p5++;
}
}
return ugly[n];
}
10. LeetCode 378. Kth Smallest Element in a Sorted Matrix
- n: the size of the n x n matrix
- k: the position of the desired element (1 ≤ k ≤ n²)
public int kthSmallest(int[][] matrix, int k) {
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> {
// 按照元素大小升序排序
return a[0] - b[0];
});
for (int i = 0; i < matrix.length; i++, i++) {
pq.offer(new int[]{matrix[i][0], i, 0});
}
// loop k times
while (!pq.isEmpty() && k > 0) {
int[] cur = pq.poll();
res = cur[0];
k--;
int i = cur[i], j = cur[j];
if (j + 1 < matrix[0].length) {
pq.add(new int[]{matrix[i][j + 1], i, j + 1})
}
}
return res;
}
-
Array of Priority Queue:
{matrix[i][j], i, j}, value, row index, column index -
Time Complexity:
- Line 7-9: n insertion x O(log n) = O(n log n)
- Insertion into heap: O(log n)
- Line 12-21
- poll(): O(log n)
- At most 1 add: O(log n) (only if the row has more elements)
- Total per iteration: O(log n) + O(log n) = O(log n)
- Total for k iterations: O(k log n)
- Line 7-9: n insertion x O(log n) = O(n log n)
-
Combined: O(n log n + k log n)
-
Since k ≤ n² (the matrix has n² elements), the worst case occurs when k = n²:
- O(n log n + n² log n) = O(n² log n)
-
However, we typically express the complexity as O(n log n + k log n) to show how it depends on both n (matrix size) and k (number of elements to process). This highlights that:
- For small k, the k log n term is small, making the algorithm efficient
- For large k (up to n²), the k log n term dominates
11. LeetCode 373. Find K Pairs with Smallest Sums
- https://leetcode.com/problems/find-k-pairs-with-smallest-sums/
- Variant of LeetCode 23. Merge K Sorted Lists
- The pairs are ordered by sum in ascending order, so we can use 23. Merge K Sorted Lists to solve this problem to loop the first kth pairs
nums1 = [1,7,11], nums2 = [2,4,6]
1: [1, 2] -> [1, 4] -> [1, 6]
2: [7, 2] -> [7, 4] -> [7, 6]
3: [11, 2] -> [11, 4] -> [11, 6]
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> {
return (a[0] + a[1]) - (b[0] + b[1]);
});
// add the head node of each list
for (int i = 0; i < nums1.length; i++) {
pq.offer(new int[]{nums1[i], nums2[0], 0});
}
// process the whole linked list
List<List<Integer>> res = new ArrayList<>();
while(!pq.isEmpty() && k > 0) {
int[] cur = pq.poll();
k--;
int nextIndex = cur[2] + 1;
if (nextIndex < nums2.length) {
pq.add(new int[]{cur[0], nums2[nextIndex], nextIndex});
}
List<Integer> list = new ArrayList<>();
pair.add(cur[0]);
pair.add(cur[1]);
res.add(pair);
}
return res;
}
- The triple:
(nums1[i], nums2[i], i) - i is used to record the index of nums2 for generating next node
12. LeetCode 2. Add Two Numbers
- Start from 個位,align with our calculation of addition
carry: used to handle 進位- Need to use Math.floor() and mod
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
let p1 = l1, p2 = l2;
let dummy = new ListNode(-1);
let p = dummy;
let carry = 0;
while (p1 != null || p2 != null || carry > 0) {
let sum = carry;
if (p1 != null) {
sum += p1.val;
p1 = p1.next;
}
if (p2 != null) {
sum += p2.val;
p2 = p2.next;
}
carry = Math.floor(sum / 10);
sum = sum % 10;
p.next = new ListNode(sum);
p = p.next;
}
return dummy.next;
}
13. LeetCode 206. Reverse Linked List
- Reverse the direction of each node
- Initilization
pre = null:cur = head:nxt = head.next:
...
while (cur != null) {
cur.next = pre;
pre = cur;
cur = nxt;
if (nxt != null) {
nxt = nxt.next;
}
}
...
14. LeetCode 445. Add Two Numbers II
- 不可用reverse linked list的方法
- instead, use Stack, FILO
- Then use method in 2. Add Two Numbers