LinkedList (Two Pointers)

Question List

ID	LeetCode	Difficulty	Date of Submission
1	21. Merge Two Sorted Lists	🟢	20250623
2	86. Partition List	🟠	20250623
3	19. Remove Nth Node From End of List	🟠	20250623
4	876. Middle of the Linked List	🟢	20250625
5	141. Linked List Cycle	🟢	20250623
6	142. Linked List Cycle II	🟠	20250623
7	160. Intersection of Two Linked Lists	🟢	20250625
8	23. Merge k Sorted Lists	🔴
9	Sword Offer 22. Kth Node From End of List	🟢
10	82. Remove Duplicates from Sorted List II	🟠	20250701
11	264. Ugly Number II	🟠
12	378. Kth Smallest Element in a BST	🟠	20250702
13	373. Find K Pairs with Smallest Sums	🟠
14	2. Add Two Numbers	🟠	20250625

LC21. Merge Two Sorted Lists

Idea

1. In while loop, compare the values of the head of two lists.
2. Use dummy head and pointer of dummy p, everytime we move the pointer p only but return the result with dummy.next.

Solution

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        // create dummy head and pointer of dummy
        ListNode dummy = new ListNode(-1), p = dummy;
        ListNode p1 = l1, p2 = l2;
        
        while (p1 != null && p2 != null) {
            if (p1.val > p2.val) {
                p.next = p2;
                p2 = p2.next;
            } else {
                p.next = p1;
                p1 = p1.next;
            }
            p = p.next;
        }
        
        if (p1 != null) {
            p.next = p1;
        }
        
        if (p2 != null) {
            p.next = p2;
        }
        
        return dummy.next;
    }
}

LC86. Partition List

Idea

1. Use two linked lists.
2. The first one to store all nodes that are less than x.
3. The second one to store all nodes that are greater than or equal to x.

Solution

class Solution {
    public ListNode partition(ListNode head, int x) {
        // less than x
        ListNode list1 = new ListNode(-1), p1 = list1;
        // greated than or equal to x
        ListNode list2 = new ListNode(-1), p2 = list2;
        ListNode p = head;

        while (p != null) {
            if (p.val < x) {
                p1.next = p;
                p1 = p1.next;
            } else {
                p2.next = p;
                p2 = p2.next;
            }

            ListNode temp = p.next;
            p.next = null;
            p = temp;
        }

        p1.next = list2.next;
        return list1.next;
    }
}

LC19. Remove Nth Node From End of List

Idea

1. Use two pointers: fast and slow.
2. The fast pointer moves n steps ahead, then fast and slow pointers move together.
3. Use dummy head in case we needs to remove the first node.
4. Find the previous node of the node to be removed.

Solution

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(-1);
        dummy.next = head;

        ListNode slow = dummy, fast = dummy;

        // n + 1 because we need to find the previous node
        for (int i = 0; i < n + 1; i++) {
            fast = fast.next;
        }

        while (fast != null) {
            slow = slow.next;
            fast = fast.next;
        }

        slow.next = slow.next.next;
        return dummy.next;
    }
}

LC141. Linked List Cycle

Idea

1. Slow pointer moves one step at a time, the fast pointer moves two steps forward.
2. If fast pointer reaches the end of the list, it means there is no cycle.
3. If fast pointer and slow pointer meet, it means there is a cycle.

Solution

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;

        while (slow != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;

            if (fast.equals(slow)) {
                return true;
            }
        }
        
        return false;
    }
}

LC142. Linked List Cycle II

Idea

1. Find the intersection node by fast and slow pointers.
2. When they intersect, slow walks k steps, and fast walks 2k steps. Fast pointer must walk k more steps than slow pointer. So, k is the multiple of the length of the cycle.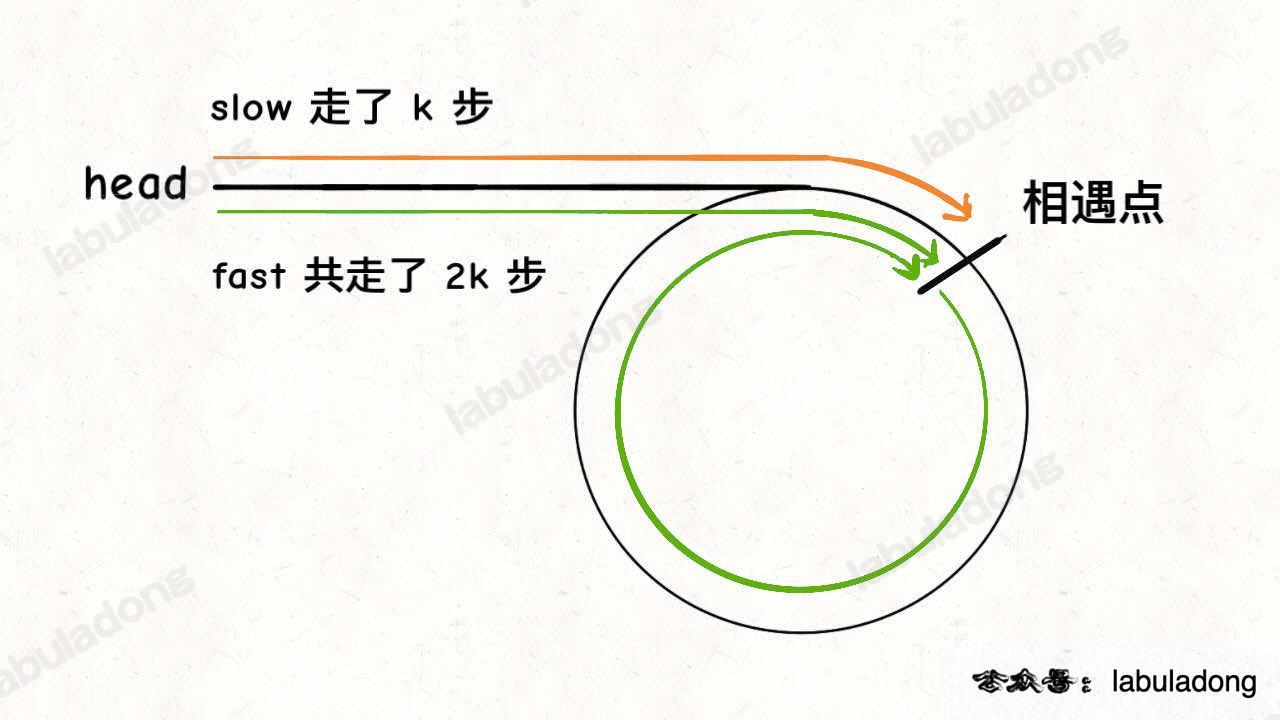
3. Reset the slow pointer to the head, and fast pointer to the intersection node.
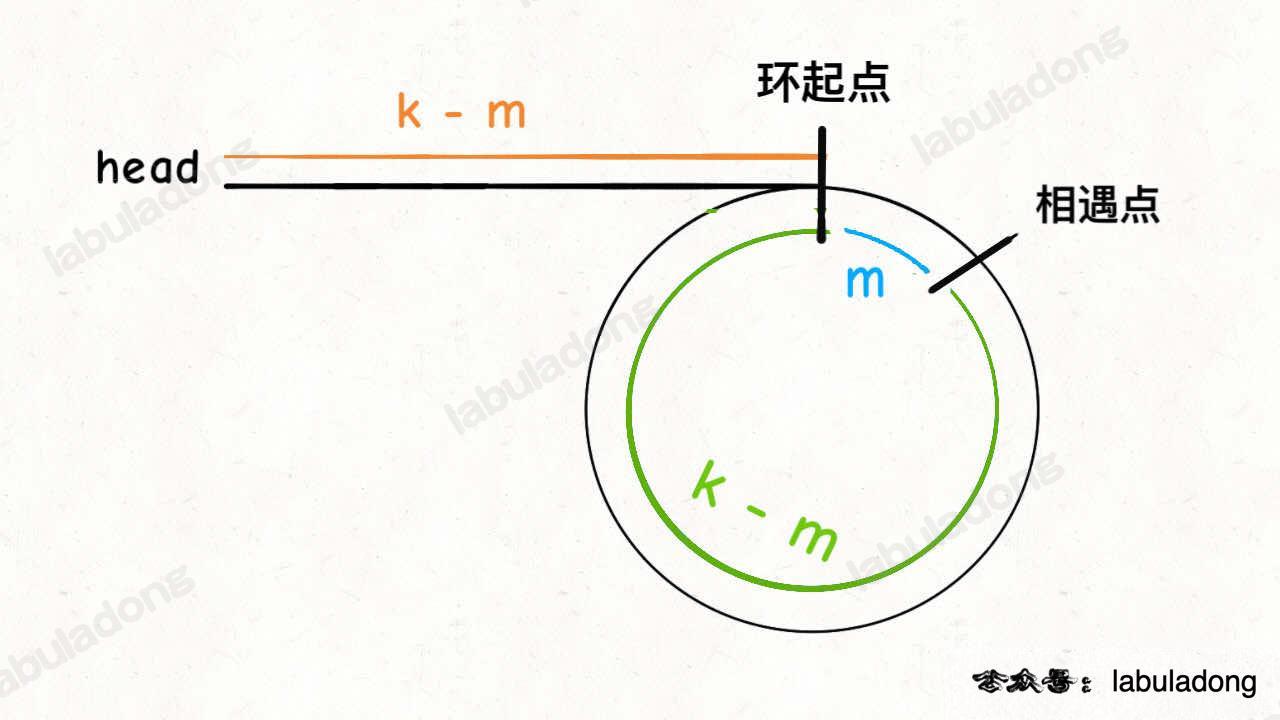
   • What is k? And Why k-m
4. Both pointers walk until they intersect, the intersection node is the start node of the cycle.

Solution

    class Solution {
        public ListNode detectCycle(ListNode head) {
            ListNode fast, slow;
            fast = slow = head;

            // termination: fast is at the end of the list/is null
            while (fast != null && fast.next != null) {
                fast = fast.next.next;
                slow = slow.next;
                if (fast == slow) break;
            }

            if (fast == null || fast.next == null) return null;

            slow = head;
            while (fast != slow) {
                fast = fast.next;
                slow = slow.next;
            }

            return slow;
        }
    }

LC160. Intersection of Two Linked Lists

Idea

1. We can let p1 traverse list A and then start traversing list B, and let p2 traverse list B and then start traversing list A. By doing this, p1 and p2 can enter the common point at the same time.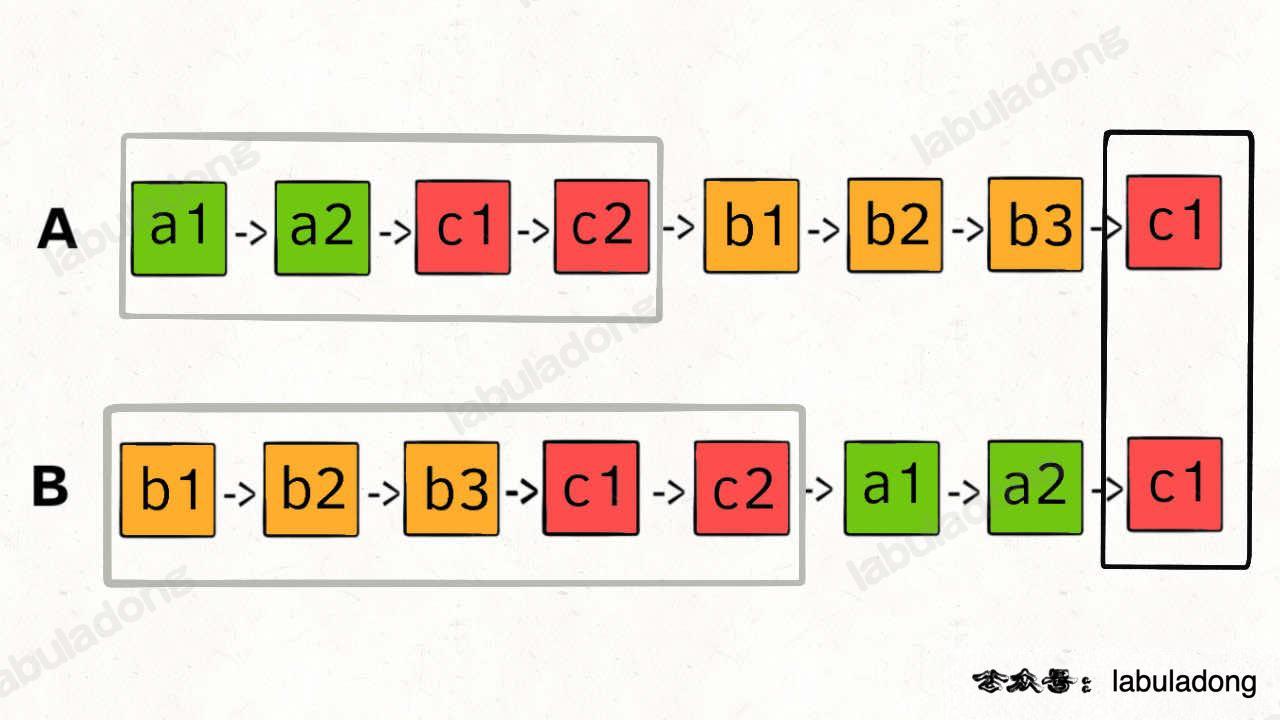

Solution

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode p1 = headA, p2 = headB;

        while (headA != null && headB != null) {
            if (p1 == null) {
                p1 = headB;
            } else {
                p1 = p1.next;
            }

            if (p2 == null) {
                p2 = headA;
            } else {
                p2 = p2.next;
            }

            if (p1 == p2) {
                return p1;
            }
        }

        return null;
    }
}

LC876. Middle of the Linked List

Idea

1. Use slow and fast pointer method. The slow pointer moves one step at a time, while the fast pointer moves two steps at a time.
2. This way, when the fast pointer reaches the end of the list, the slow pointer will be in the middle.
3. Be noted that if the linked list has an even number of nodes, meaning there are two middle nodes, the solution returns the latter of the two middle nodes.

Solution

class Solution {
    public ListNode middleNode(ListNode head) {
        ListNode fast = head, slow = head;

        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }

        return slow;
    }
}

LC2. Add Two Numbers

Idea

1. Use carry to handle the carry in addition operation.

Solution

    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        let p1 = l1, p2 = l2;
        let dummy = new ListNode(-1);
        let p = dummy;

        let carry = 0;

        // termination: arrive the end of two linked lists, and carry == 0
        while (p1 != null || p2 != null || carry > 0) {
            // add carry first, and then the value of two nodes
            let val = carry;
            if (p1 != null) {
                val += p1.val;
                p1 = p1.next;
            }

            if (p2 != null) {
                val += p2.val;
                p2 = p2.next;
            }

            // handle carry
            carry = val / 10;
            val = val % 10;

            p.next = new ListNode(val);
            p = p.next;
        }

        return dummy.next;
    }

LC82. Remove Duplicates from Sorted List II

Idea

1. We can use two linked lists, one is for the deplicated list, one is for the unique list.
   • If current node and next node have the same value, put the current node into DuplicateList.
   • If value of current node is in the DuplicateList, put the current node into DuplicateList.
2. Need to set the next node of DuplicateList and UniqueList to null.

Solution

    class Solution {
        public ListNode deleteDuplicates(ListNode head) {
            ListNode dummyUniq = new ListNode(101);
            ListNode dummyDup = new ListNode(101);

            ListNode pUniq = dummyUniq, pDup = dummyDup;
            ListNode p = head;

            while (p != null) {
                if ((p.next != null && p.val == p.next.val) || p.val == pDup.val) {
                    pDup.next = p;
                    pDup = pDup.next;
                } else {
                    pUniq.next = p;
                    pUniq = pUniq.next;
                }

                p = p.next;
                pUniq.next = null;
                pDup.next = null;
            }

            return dummyUniq.next;
        }
    }

LC264. Ugly Number II

Idea

1. This question is removed.
2. Ugly Number: with prime factors only 2, 3, 5
3. Expected linked list: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 8 -> ...
4. Think it as linked list

   2: 1 -> 1*2 -> 2*2 -> 3*2 -> 4*2 -> 5*2 -> 6*2 -> 8*2 -> ...
   3: 1 -> 1*3 -> 2*3 -> 3*3 -> ...
   5: 1 -> 1*5 -> 2*5 -> 3*5 -> ...

• 把這3條有序的linked list合併，need to remove duplicated value, e.g. 2*3 and 3*2

Solution

    public int nthUglyNumber(int n) {
        // pointer to the head of each linked list
        int p2 = 1, p3 = 1, p5 = 1;
        // the value of the head node of each linked list
        int product2 = 1, product3 = 1, product5 = 1;
        // the final merged linked list
        int[] ugly = new int[n + 1];
        // the pointer to the merged linked list
        int p = 1;

        while (p <= n) { 
            int min = Math.min(product2, Math.min(product3, product5));

            // add the result list
            ugly[p] = min;
            p++;

            // if the node is selected from the 2nd list, then move the pointer to the next node in 2nd list
            // if the value of head node of any other list is equal to the value of the selected node, then move the pointer to the next node in that list as well

            if (min == product2) {
                product2 = 2 * ugly[p2];
                p2++;
            }
            if (min == product3) {
                product3 = 3 * ugly[p3];
                p3++;
            }
            if (min == product5) {
                product5 = 5 * ugly[p5];
                p5++;
            }
        }

        return ugly[n];
    }

LC378. Kth Smallest Element in a Sorted Matrix

Idea

1. Use PriorityQueue to store the tuple {matrix[i][j], i, j}, value, row index, column index

Code

    public int kthSmallest(int[][] matrix, int k) {
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> {
            // 按照元素大小升序排序
            return a[0] - b[0];
        });

        for (int i = 0; i < matrix.length; i++, i++) {
            // {matrix[i][j], i, j}, value, row index, column index
            pq.offer(new int[]{matrix[i][0], i, 0});
        }

        // loop k times: when k == 0, we have found the kth smallest element
        while (!pq.isEmpty() && k > 0) {
            int[] cur = pq.poll();
            res = cur[0];
            k--;

            // add next element from the same linked list
            int i = cur[1], j = cur[2];
            if (j + 1 < matrix[0].length) {
                pq.add(new int[]{matrix[i][j + 1], i, j + 1})
            }
        }

        return res;
    }

Complexity Analysis

• Time Complexity:

  1. Line 7-9: n insertion x O(log n) = O(nlogn)
     • Insertion into heap: O(log n)
  2. Line 13-23
     • poll(): O(log n)
     • At most 1 add: O(log n) (only if the row has more elements)
     • Total per iteration: O(log n) + O(log n) = O(log n)
     • Total for k iterations: O(klogn)

• Combined: O(n log n + k log n)

• Since k ≤ n² (the matrix has n² elements), the worst case occurs when k = n²:

  • O(n log n + n² log n) = O(n² log n)

• However, we typically express the complexity as O(n log n + k log n) to show how it depends on both n (matrix size) and k (number of elements to process). This highlights that:

  • For small k, the k log n term is small, making the algorithm efficient
  • For large k (up to n²), the k log n term dominates

LeetCode 373. Find K Pairs with Smallest Sums

Idea

• Variant of LeetCode 23. Merge K Sorted Lists
• The pairs are ordered by sum in ascending order, so we can use 23. Merge K Sorted Lists to solve this problem to loop the first kth pairs

    nums1 = [1,7,11], nums2 = [2,4,6]

    1: [1, 2] -> [1, 4] -> [1, 6]
    2: [7, 2] -> [7, 4] -> [7, 6]
    3: [11, 2] -> [11, 4] -> [11, 6]

Code

    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> {
            return (a[0] + a[1]) - (b[0] + b[1]);
        });

        // add the head node of each list
        for (int i = 0; i < nums1.length; i++) {
            // (nums1[i], nums2[j], j)
            pq.offer(new int[]{nums1[i], nums2[0], 0});
        }
        
        // process the whole linked list
        List<List<Integer>> res = new ArrayList<>();
        while(!pq.isEmpty() && k > 0) {
            int[] cur = pq.poll();
            k--;

            int nextIndex = cur[2] + 1;
            if (nextIndex < nums2.length) {
                pq.add(new int[]{cur[0], nums2[nextIndex], nextIndex});
            }

            List<Integer> pair = new ArrayList<>();
            pair.add(cur[0]);
            pair.add(cur[1]);
            res.add(pair);
        }
        return res;
    }

• The triple: (nums1[i], nums2[j], j)
• i is used to record the index of nums2 for generating next node